1. 数字表示基础

unsetunset1.1 二进制与十进制转换unsetunset

在计算机的世界里，所有的数据都是以二进制的形式存储的。二进制只有两个数字：0 和 1。而我们日常生活中习惯用十进制，它有十个数字：0 到 9。这两种进制之间的转换就像是不同语言之间的翻译。

以十进制的数字 13 为例，转换成二进制是 1101。这个过程就像是把一个十进制的“蛋糕”切成二进制的“小块”。具体来说，13 除以 2，商是 6，余数是 1（这是二进制的最低位），6 再除以 2，商是 3，余数是 0，3 除以 2，商是 1，余数是 1，最后 1 除以 2，商是 0，余数是 1（这是二进制的最高位）。把这些余数倒过来写，就是 1101。箭头指示余数排列方向：↑1 ↑0 ↑1 ↑1 → 倒序排列为1101

反过来，从二进制 1101 转换回十进制，就像是把这些“小块”重新拼成“蛋糕”。从右到左，每一位的权重是 2 的幂次方，最右边是 ，然后是 、、。所以，1101 就是 1×+1×+0×+1×=8+4+0+1=13。

unsetunset1.2 浮点数与整数区别unsetunset

（一）整数类型（INT）

INT 是 Integer 的缩写，即整数类型。整数就像是数数时用的数字，比如 1、2、3……没有小数部分。

INT4 表示用 4 位二进制数来表示一个整数，INT8 则是用 8 位二进制数表示整数。

例如，INT4 能够表示的整数范围是有限的，因为 4 位二进制数最多能表示 =16 个不同的数 ，如果是有符号数，范围通常是 -8 到 7；如果是无符号数，范围就是 0 到 15。而 INT8 有符号数范围是 -128 到 127，无符号数范围是 0 到 255 ，因为 8 位二进制数能表示 = 256 个不同的数。

（二）浮点数类型（FP）

FP 是 Floating Point 的缩写，也就是浮点数类型。浮点数用于表示带有小数部分的数。

它由三部分组成：符号位、指数位和尾数位。以 32 位浮点数（FP32）为例，它有 1 位符号位（表示正负）、8 位指数位和 23 位尾数位。这种表示方式可以让浮点数表示的范围非常大，从非常小的数到非常大的数，就像一个可以伸缩的尺子。

举个例子，FP32 可以表示像 这样小的数，也可以表示像 这样大的数。而 INT8（8 位整数）只能表示从 -128 到 127 的整数。这种差异就像是用一把直尺（整数）和一把可以伸缩的卷尺（浮点数）来测量距离。

unsetunset（三）常用的数据类型unsetunset

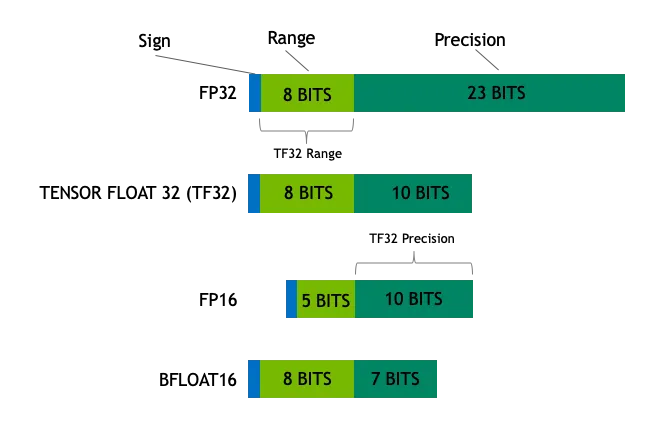常见的数据类型有：

• Float32 (FP32)：这是标准的32位浮点数，精度高，能表示的数值范围大。大部分硬件都支持FP32运算，所以在训练和推理中广泛使用。
• Float16 (FP16)：这是16位浮点数，精度比FP32低，但占用的内存少，计算速度快。FP16的数值范围较小，容易出现上溢和下溢的问题，但在深度学习中可以通过一些技巧来缓解这些问题。
• Bfloat16 (BF16)：这是另一种16位浮点数，它的指数位数和FP32相同，所以动态范围较大，但精度比FP16低。BF16在处理大数值时表现更好，但在精度上会有所损失。
• Int8：这是8位整数类型，能存储的数值范围有限，但占用的内存更少。Int8主要用于模型量化，通过将模型参数从FP32或FP16转换为Int8，可以大幅减少模型的内存占用和计算量。

2. 量化概念

unsetunset2.1 量化定义unsetunset

量化就像是把一幅高精度的画变成一幅低精度的画，但尽量让它看起来还差不多。在计算机的世界里，量化是指将模型中的数据从高精度表示转换为低精度表示。比如，把 FP32（32 位浮点数）转换成 FP16（16 位浮点数）或 INT8（8 位整数）。

FP32 是一种高精度的浮点数，它有 1 位符号位、8 位指数位和 23 位尾数位，总共 32 位。它可以表示非常大和非常小的数，就像一把非常精确的尺子，但缺点是占用的存储空间大，计算速度慢。

而 FP16 是一种低精度的浮点数，它有 1 位符号位、5 位指数位和 10 位尾数位，总共 16 位。它的精度比 FP32 低，但占用的存储空间少了一半，计算速度也更快。就像把尺子的刻度变粗一些，虽然精度降低了，但使用起来更方便。

再比如 INT8，它是一个 8 位的整数，只能表示从 -128 到 127 的整数。它的存储空间更小，计算速度也更快，但精度更低。就像用一个简单的计数器代替精确的尺子，虽然只能数整数，但速度更快。

unsetunset2.2 量化目的unsetunset

量化的主要目的是为了减少模型的存储需求和计算复杂度，同时尽量减少精度损失。具体来说：

减少存储需求：大模型通常包含数亿甚至数十亿个参数，占用大量的存储空间。比如，一个使用 FP32 的模型，每个参数占用 4 个字节。如果将它量化为 FP16，每个参数只需要 2 个字节，存储需求直接减半。如果进一步量化为 INT8，每个参数只需要 1 个字节，存储需求减少了 75%。

提高计算效率：量化后的模型在推理时的计算量更少，能够加快推理速度。例如，使用 FP32 的模型在 GPU 上运行时，计算速度可能受到限制。而使用 FP16 或 INT8 的模型，由于硬件对低精度计算的优化，计算速度可以显著提升。在边缘设备或移动设备上，计算资源有限，量化能带来明显的性能提升。

降低功耗：量化后的模型需要的计算资源更少，从而降低了能耗。在移动设备和嵌入式系统中，功耗是一个重要考虑因素。量化后的模型可以延长设备的使用时间，同时减少散热需求。

减少带宽需求：在分布式系统中，模型大小的减小也意味着传输所需的带宽减少。比如，在多台服务器之间传输模型时，量化后的模型可以更快地完成传输，提高数据传输效率。

3. INT4、INT8量化

unsetunset3.1 INT4与INT8表示范围unsetunset

INT4和INT8都是整数类型的量化方式，它们在计算机中以二进制形式存储数据，但表示的范围和精度有所不同。

• INT8：它是一个8位整数，能够表示的范围是从-128到127。这就好比你有一个8位的计数器，每一位可以是0或1，通过不同的组合来表示不同的整数。例如，二进制的00000000表示十进制的0，而11111111表示十进制的-1（在补码表示法中）。这种表示方式在很多场景下已经足够用了，比如图像处理中的像素值，通常在0到255之间，用INT8就可以很好地表示。

• INT4：它是一个4位整数，表示的范围更小，从-8到7。虽然它的范围有限，但存储空间更小，计算速度更快。这就像你有一个更小的计数器，虽然能表示的数字范围变小了，但它的“体积”也更小，使用起来更节省空间。在一些对精度要求不是特别高的场景，比如某些简单的神经网络层，使用INT4可以大大减少存储和计算成本。

unsetunset3.2 量化公式与示例unsetunset

量化的过程就是将高精度的浮点数转换为低精度的整数。以FP32（32位浮点数）量化为INT8为例，具体的量化公式如下：

其中：

•  是原始的浮点数。
•  是量化后的整数。
• 是缩放因子，用于将浮点数映射到整数范围。
• 表示四舍五入到最近的整数。
• 表示将结果限制在INT8的范围内，即［－128，127］。

计算缩放因子

缩放因子 scale 的计算方式通常是根据浮点数的最大绝对值来确定的。假设我们有一组浮点数   ，计算步骤如下：

1．找出这组浮点数的最大绝对值    。 2．计算缩放因子  。

示例

假设我们有一组浮点数 ，我们来逐步完成量化过程：

1．计算最大绝对值：

2．计算缩放因子：

3．量化每个浮点数：

• 对于 -0.5 ：

• 对于 0.3 ：

• 对于 1.2 ：

• 对于 -2.1 ：

最终，量化后的INT8表示为 。

通过这个过程，我们可以看到量化是如何将浮点数转换为整数的。虽然量化会带来一定的精度损失，但通过合理选择缩放因子，可以在减少存储和计算成本的同时，尽量保持模型的性能。

4. FP8、FP16、FP32量化

unsetunset4.1 FP8、FP16、FP32表示方法unsetunset

FP8、FP16 和 FP32 都是浮点数的表示方式，它们在计算机中以二进制形式存储，但位数不同，因此表示范围和精度也不同。

FP32

FP32 是一种标准的 32 位浮点数，它由三部分组成：

• 符号位（1 位）：表示数字的正负，0 表示正数，1 表示负数。

• 指数位（8 位）：用于表示数字的大小范围，可以表示从非常小到非常大的数。

• 尾数位（23 位）：用于表示数字的精度部分，决定了浮点数的精度。

FP32 的表示范围非常广泛，从大约 到 ，精度可以达到小数点后 6 位左右。这就好比用一把非常精确的尺子来测量距离，可以测量从微小的灰尘到巨大的山脉。

FP16

FP16 是一种半精度浮点数，它占用的空间是 FP32 的一半，只有 16 位。它的结构如下：

• 符号位（1 位）：表示正负。

• 指数位（5 位）：表示数字的大小范围。

• 尾数位（10 位）：表示数字的精度。

FP16 的表示范围从大约 到 ，精度相对较低，只能达到小数点后 3 位左右。这就好比把 FP32 的尺子的刻度变粗一些，虽然精度降低了，但使用起来更节省空间和时间。

FP8

FP8 是一种新兴的低精度浮点数格式，主要用于深度学习中的高效计算。它通常有以下结构：

• 符号位（1 位）：表示正负。

• 指数位（3 位或 4 位）：表示数字的大小范围。

• 尾数位（4 位或 3 位）：表示数字的精度。

FP8 的表示范围和精度进一步降低，但它的优势在于占用的存储空间更小，计算速度更快。这就好比用一个非常简单的计数器来代替精确的尺子，虽然只能表示有限的数字，但速度更快，更适合在资源受限的环境中使用。

4.2 量化过程与公式

量化的过程就是将高精度的浮点数转换为低精度的浮点数或整数。以 FP32 量化为 FP16 为例，具体的量化公式如下：

其中：

•  是原始的浮点数。
•  是量化后的低精度浮点数。
• 是缩放因子，用于将浮点数映射到低精度范围。
• 表示四舍五入到最近的值。

计算缩放因子

缩放因子 scale 的计算方式通常是根据浮点数的最大绝对值来确定的。假设我们有一组浮点数    ，计算步骤如下：

1．找出这组浮点数的最大绝对值

2．计算缩放因子

 ，其中   是目标低精度格式的最大表示值。对于 FP16，这个值是 65504。

示例

假设我们有一组 FP32 浮点数 ，我们来逐步完成量化为 FP16 的过程：

1．计算最大绝对值：

2．计算缩放因子：

3．量化每个浮点数：

• 对于 -0.5 ：

• 对于 0.3 ：

• 对于 1.2 ：

• 对于 -2.1 ：

最终，量化后的 FP16 表示为    。

通过这个过程，我们可以看到量化是如何将高精度的浮点数转换为低精度的浮点数的。虽然量化会带来一定的精度损失，但通过合理选择缩放因子，可以在减少存储和计算成本的同时，尽量保持模型的性能。

5. 量化应用与优势

unsetunset5.1 在深度学习中的应用unsetunset

量化技术在深度学习领域有着广泛的应用，尤其在模型的训练和推理阶段。以下是几种主要的应用场景：

模型训练加速

在模型训练过程中，使用低精度数据类型如 FP16 或 FP8 可以显著加快训练速度。例如，NVIDIA 的 Hopper 架构 GPU 支持 FP8 精度的 Tensor Core 计算，与传统的 FP32 训练相比，FP8 训练速度可以提升 2-3 倍。这种加速对于大规模模型的训练尤为重要，因为它可以大幅减少训练时间和计算资源的消耗。

以大模型训练为例，Inflection AI 的 Inflection2 模型采用了 FP8 混合精度在 5000 个 NVIDIA Hopper 架构 GPU 上进行训练，累计浮点运算次数高达约 1025 FLOPs。与同属训练计算类别的 Google 旗舰模型 PaLM 2 相比，在多项标准人工智能性能基准测试中，Inflection-2 展现出了卓越的性能。

模型推理优化

在模型推理阶段，量化可以显著降低模型的存储需求和计算复杂度。例如，将 FP32 模型量化为 INT8，存储需求可以减少 75%，推理速度可以提升数倍。这对于在边缘设备或移动设备上部署模型尤为重要，因为这些设备的计算资源和存储空间通常有限。

例如，Google 与 NVIDIA 团队合作，将 TensorRT-LLM 应用于 Gemma 模型，并结合 FP8 技术进行了推理加速。使用 Hopper GPU 进行推理时，FP8 对比 FP16 在吞吐量上能够带来 3 倍以上的收益。

模型压缩与部署

量化还可以用于模型的压缩和部署。通过将高精度模型量化为低精度模型，可以减少模型的大小，从而更容易将模型部署到资源受限的环境中。例如，零一万物基于 NVIDIA 软硬结合的技术栈，完成了在大模型的 FP8 训练和验证。其大模型的训练吞吐相对 BF16 得到了 1.3 倍的性能提升。

量化后的模型不仅在存储和计算上具有优势，还可以通过特定的硬件加速来进一步提升性能。例如，NVIDIA 的 Transformer Engine 已经集成到 PyTorch、JAX、PaddlePaddle 等基础深度学习框架中，为量化模型的推理提供了高效的硬件支持。

unsetunset5.2 优势与局限性unsetunset

优势

计算效率提升：低精度量化可以显著加快计算速度，减少计算资源的消耗。例如，FP16 和 FP8 的计算吞吐量比 FP32 高出数倍。这种加速效果在大规模模型训练和推理中尤为明显。

：量化可以大幅减少模型的存储需求。例如，将 FP32 模型量化为 INT8，存储需求可以减少 75%。这对于在资源受限的环境中部署模型非常有帮助。

功耗降低：低精度计算需要的计算资源更少，从而降低了能耗。在移动设备和嵌入式系统中，功耗是一个重要考虑因素。量化后的模型可以延长设备的使用时间，同时减少散热需求。

模型优化：量化促使模型在训练和推理过程中进行优化和压缩，进一步降低部署成本。例如，FP8 的使用可以促使模型在训练过程中进行更细致的量化，从而提高模型的效率。

局限性

精度损失：量化会带来一定的精度损失，尤其是在低精度格式下。例如，FP8 的精度比 FP16 和 FP32 低，可能会在某些任务中导致性能下降。虽然通过合理选择缩放因子可以在一定程度上减少精度损失，但完全避免精度损失是不可能的。

硬件支持有限：并非所有硬件都支持低精度计算。例如，FP8 和 FP16 的计算需要特定的硬件支持，如 NVIDIA 的 Hopper 架构 GPU。如果硬件不支持低精度计算，量化的优势将无法充分发挥。

复杂性增加：量化过程本身会增加模型的复杂性。例如，在量化过程中需要计算缩放因子，并且需要对模型进行校准和调整。这可能会增加模型开发和部署的难度。

适用场景有限：量化并不适用于所有场景。例如，在需要高精度计算的任务中，如某些科学计算或金融建模任务，量化可能会导致不可接受的精度损失。

通过以上分析，我们可以看到量化技术在深度学习中的应用非常广泛，它在提高计算效率、降低存储需求和功耗等方面具有显著优势。然而，量化也存在一定的局限性，如精度损失和硬件支持有限等。因此，在实际应用中，需要根据具体需求和场景，合理选择量化策略，以达到最佳的性能和效率平衡。